Asymmetric edge transport and topological obstruction to Anderson localization

A comment that sometimes appears in the literature asserts that the absence of back-scattering is 'protected topologically'. The paper Topological protection of perturbed edge states [B. Comm. Math. Sci. 2019] revisits this question. This paper introduces a class of two-dimensional Hamiltonians to describe transport in the vicinity of a vertical edge of interest parametrized by \(x=0\). An analytic Noether (Fredholm) index is assigned to each Hamiltonian in the form \(M_\tau-N_\tau\), which can be related to the difference of topological invariants (Chern numbers) of the bulks on the left and right of the edge.

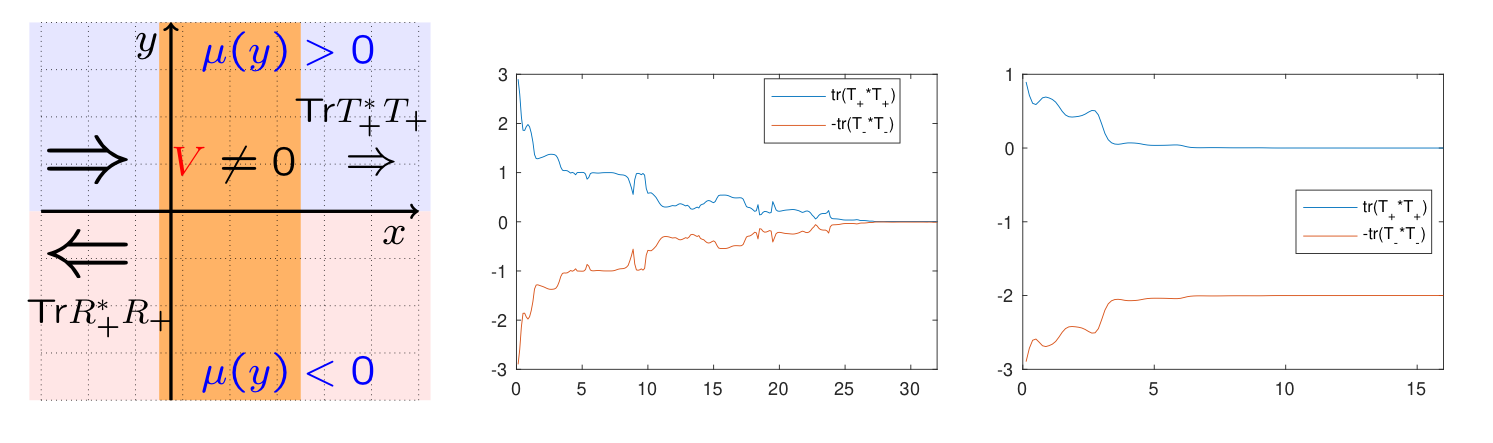
A scattering theory next quantifies transport along the vertical edge \(x=0\). We analyze the influence of the non-trivial topology on the scattering coefficients. In particular, we show that transmission in one direction is bounded from below by \(M_\tau-N_\tau\geq0\) independent of the strength of random perturbations. This provides a surprising obstruction to Anderson localization. Moreover, such an obstruction is quantized. For an appropriate model of random fluctuations, we show that in the presence of strong perturbations, transmission is asymptotically given by \(M_\tau-N_\tau\). This implies that a number \(M_\tau-N_\tau\) of randomness-dependent modes transmit through the random medium while all other modes (asymptotically) purely reflect. Transmission in the opposite direction is asymptotically also suppressed, as expected from Anderson localization; see figure below.

Asymmetric transport requires systems that break time reversal symmetry. For time-reversal symmetric materials, \(M_\tau-N_\tau=0\) necessarily. For systems satisfying a Fermionic Time Reversal Symmetry (FTRS; typically valid in electronic systems), involving an anti-Hermitian operator \({\cal T}\) such that \({\cal T}^2=-1\), the above results extend to the setting where a \({\mathbb Z}_2\) index is defined as \( M_\tau{\rm mod } 2\). When \(M_\tau\) is odd, the system is topologically non-trivial and non-trivial transmission is guaranteed in both directions, again as a violation of Anderson localization. When \(M_\tau\) is even, the FTRS is not sufficiently strong to prevent mode coupling and complete Anderson localization in the presence of strong fluctuations.

Quantitative edge transport, integral formulations, time-dependent picture

Beyond their topological properties, there is also considerable interest to obtain quantitative estimates of such interface transport. This led to the development of integral formulations for the interface problem. An integral formulation analyzing volumetric perturbations of a Dirac model is presented in Asymmetric transport computations in Dirac models of topological insulators [B. Hoskins Wang, J. Comp. Phys. 2023]. The numerical framework was generalized to \({\mathbb Z}_2\) invariants in \({\mathbb Z}_2\) classification of FTR symmetric differential operators and obstruction to Anderson localization. The latter work also revisits quantitative obstructions to Anderson localization and shows for a large class of problems that the \({\mathbb Z}_2\) index is non-trivial if and only if edge transport cannot be gapped by continuous deformations.

Integral formulations for Klein Gordon and Dirac operators with piece-wise constant coefficients are introduced in Integral formulation of Klein-Gordon singular waveguides and in Integral formulation of Dirac singular waveguides, respectively. These formulations provide an interesting theoretical tool to analyze interface scattering problems and an incredibly efficient one to simulate them numerically.

The construction of topological invariants for interface Hamiltonians is purely spectral. Topological invariants are typically constructed to be immune to (spatially) compactly supported perturbations. This robustness to such deformations heuristically means that topology encodes large scale features. Such features cannot be tested by (finite) time dependent problems that typically probe a bounded part of the Euclidean plane. Yet, localized wavepackets are still expected to reflect the non-trivial topology of the system they probe. This behavior is analyzed in a series of recent papers devoted to the propagation of wavepackets localized near an interface separating insulators in the semi-classical regime; see Edge state dynamics along curved interfaces [B. Becker Drouot Fermanian-Kammerer Lu Watson SIMA 2023], Magnetic slowdown of topological edge states [B. Becker Drouot CPAM 2023], as well as Semiclassical propagation along curved domain walls [B. MMS 2023].

Classification by domain walls and Bulk-Edge Correspondence

In order to model asymmetric transport for more general models than Dirac systems, we first need a physical observable that characterizes such transport. The following observable, first introduced in work by Schulz-Baldes and collaborators and work by Graf and collaborators, is now ubiquitous, in a form or another, in mathematical analyses of edge transport: \[ \sigma_I = {\rm Tr} \ i[H,P] \varphi'(H). \] Here, \(H\) is the Hamiltonian of interest, \(P=P(x)\) is intuitively a function equal to \(1\) for \(x>x_0\) and equal to \(0\) otherwise (the plane is parametrized by \((x,y)\)). The operator \(i[H,P]\) then affords an interpretation as a current operator (amount of signal propagating from the left to the right of the line \(x_0\) per unit time). The function \(\varphi'(H)\geq0\) and integrating to \(1\) should be interpreted as a density of states selecting an energy (or frequency) range of excitations that cannot propagate into the insulating bulks. Thus, \(\sigma_I\), with \({\rm Tr}\) operator trace on \(L^2\), is the expected value of the operator \(i[H,P]\) for the density of states \(\varphi'(H)\geq0\). It turns out that \(\sigma_I\) is quantized in many settings of interest. Moreover, if \(I^N\) and \(I^S\) are two bulk invariants associated to the two insulators north and south of the interface \(\{y=0\}\), then the Bulk-Edge Correspondence states after appropriate orientation that \[ 2\pi \sigma_I = I^N-I^S \in {\mathbb Z}. \] The bulk edge correspondence is a central principle in the physical interpretation of topological insulators. Its derivation remains difficult independently of the context in which it applies. Most works on the bulk-edge correspondence in fact relate edge transport along a boundary to the bulk invariant in the volume (say \(I^N\) with then \(I^S\) set to \(0\)). It has been derived rigorously mathematically in many discrete settings, using either algebraic K-theory techniques generalizing Belissard's original work or more analytical techniques generalizing the Avron-Seiler-Simon theory. It was also generalized to continuous settings where bulk invariants are naturally defined.

For many differential problems, including the ubiquitous systems of Dirac equations, \(I^N\) or \(I^S\) are not naturally defined. However, their difference \(I^N-I^S\), the only quantity that appears in the bulk edge correspondence, often makes sense as a Bulk-difference invariant. This reflects a well-known fact that (topological) phase differences are defined more generally than absolute phases.

A general classification of elliptic partial differential operators and a derivation of the bulk-edge correspondence in this setting is proposed in the papers Topological invariants for interface modes [B. Comm. PDE 2022], generalized in Approximations of interface topological invariants [Quinn B. SIMA 2024], and extended to arbitrary dimension (and Higher-Order Topological Insulators) in Topological charge conservation for continuous insulators [B. J. Math. Phys. 2023]. The salient features of the results in these papers is summarized as follows.

For \(H_k\) an elliptic operator assumed to be confined in \(0\leq k\leq d-1\) dimensions in a \(d-\)dimensional Euclidean space, the two operator \[ H_{d-1} = \gamma_0 \otimes H_k + \mu(x) \cdot \gamma \otimes I,\quad \mbox{ and } \quad F = H_{d-1} -i\mu(x_d), \] are constructed using known Clifford matrices \(\gamma_0\) and \(\gamma\) and domain walls \(\mu(x)\). The operator \(H_{d-1}\) is an interface Hamiltonian similar to the ones described above when \(d=2\). The main advantage of the procedure is that \(F\) is a Fredholm operator. Writing \(F={\rm Op}^w a\) with \(a\) the matrix-valued Weyl symbol of \(F\), which may be written explicitly in terms of the Weyl symbol of the initial operator \(H_k\), we associate to \(H_k\) the topological invariant \[ {\mathbb Z} \ni {\rm Index} \,F = - \frac{(d-1)!}{(2\pi i)^d (2d-1)!} \int_{{\mathbb S}^{2d-1}_R} {\rm tr}\, (a^{-1} da)^{\wedge(2d-1)}. \] Here, \(R\) is chosen large enough that \(a^{-1}\) is defined outside of the ball of radius \(R\) (in phase space). This is the Fedosov-Hörmander formula, which implements in Euclidean spaces an Atiyah-Singer index theory.

This invariant is defined for a large class of Hamiltonians \(H_k\) as a generalized winding number of its Weyl symbol. It is also defined for non-Hermitian operators \(H_k\) so long as \(a^{-1}\) is indeed defined as above. It may thus also serve to classify non-Hermitian operators (in the symmetry classes A and AIII).

For Hermitian operators, the above papers prove a Bulk-Edge Correspondence of the form: \[ \mbox{ Theorem (Generalized Bulk-Edge Correspondence)}: \quad 2\pi \sigma_I[H_{d-1}] = {\rm Index} \,F. \] In dimension \(d=2\) with interface Hamiltonian \(H=H_1\), the above formula simplifies as an application of the Stokes theorem (since \(d{\rm tr}\,(a^{-1}da) ^{\wedge 3} =0\)) to \[ 2\pi \sigma_I[H] = {\rm Index} \,F = \frac{1}{24\pi^2}\int_{{\mathbb S}_R^3} {\rm tr}\ (a^{-1}da) ^{\wedge 3} = \frac{1}{24\pi^2}\int_{\{y=R\} \cup \{y=-R\}} {\rm tr}\ (a^{-1}da) ^{\wedge 3}. \] In other words, the edge current observable \(2\pi \sigma_I[H] \), which is a priori difficult to compute, simply depends on the symbol of \(H\) in the insulating bulks (at \(y=\pm R\)). This remarkable identity, which is natural in light of the Atiyah-Singer index theory, allows one to considerably simplify the computation of the edge invariant as a simple integral.

The integral further simplifies assuming bulk Hamiltonians invariant under translation for \(|y|\) sufficiently large. Writing phase space in the variables \((x,y,\xi,\zeta)\), we may introduce \[ {-a(\omega,y=\pm R,\xi,\zeta) = (i\omega- \hat H_B^{N/S}(\xi,\zeta)) ,\qquad \Pi^{N/S}(\xi,\zeta)=\chi(\hat H_B^{N/S}(\xi,\zeta)<0)} . \] Here, \(\Pi^{N/S}(\xi,\zeta)\) are families of projection operators onto the negative spectrum of the (North and South) bulk Hamiltonians \(\hat H_B^{N/S}(\xi,\zeta)\) in Fourier variables. We then show that \[ 2\pi\sigma_I= \frac{i}{2\pi} \int_{{\mathbb R}^2} {\rm tr} \big( \Pi^S[\partial_1 \Pi^S,\partial_2\Pi^S] - \Pi^N[\partial_1 \Pi^N,\partial_2\Pi^N]\big) d\xi d\zeta \] written as Bulk-difference invariant. The above expression follows the standard construction of Chern numbers on the unit sphere obtained by circle compactification of the two Fourier planes.

Bulk-Edge Correspondence (or not), spectral flows, and ellipticity

Note that the Fedosov-Hörmander formula provides a significantly simpler means to compute the edge current \(2\pi\sigma_I \) than the spectral flow \({\rm SF}[H]\), which requires a complete diagonalization of the operator \(H\) restricted to the support of \(\varphi'(E)\).

The same notion of spectral flow has been used in the analysis of asymmetric atmospheric mass transport along the earth's equator, which was given a topological interpretation in a 2017 Science paper by Delplace-Marston-Venaille. The insulating bulk phases result from a Coriolis force parameter that is non-vanishing in the northern and southern poles but changes signs in the vicinity of the equator. This model involves a flat band (infinitely degenerate point spectrum at frequency \(E=0\)).

Surprisingly, the bulk-edge correspondence does not fully apply in that setting in the sense that the current observable \(2\pi\sigma_I = {\rm SF}[H]\) depends on the way the Coriolis force parameter transitions from the Northern to the Southern hemispheres. In particular, when the Coriolis force parameter is proportional to the latitude variable \(y\), then \(2\pi\sigma_I = {\rm SF}[H]=2\), which is the `correct' value we expect from the bulk-edge correspondence. In contrast, we observe that \(2\pi\sigma_I = {\rm SF}[H]=1\) when the Coriolis force parameter equals the sign function of \(y\). See [B. Comm. PDE 2022] and [Quinn B. SIMA 2024] for details. A forthcoming work in collaboration with Jiming Yu shows that \(2\pi\sigma_I\) may in fact take any value in \({\mathbb Z}\) for discontinuous profiles of the Coriolis force parameter. However, when the latter is sufficiently smooth, then \(2\pi\sigma_I=2\) as per the bulk-edge correspondence.

Hybrid Inverse Problems.

Limiting models for Equations with stochastic coefficients.

Kinetic Models and Imaging.

Time Reversal.

Links to Talks and Lecture Notes

Inverse Transport Theory.

Ray transforms and X-Ray Tomography.

Optical Tomography.

Physical modeling of noise and random correctors in inverse problems.