Homework 5: due Wednesday 5/14

1. FPPA, Chapter 16, Review Exercises 2, 3, 6, 7.
2. FPPA, Chapter 17, Review Exercises 2, 6, 8, 9.
3. FPPA, Chapter 18, Review Exercises 7, 8, 9, 10.

Homework 4: due Wednesday 4/30

1. FPPA, Chapter 11, Review Exercises 3, 4, and 6.
2. FPPA, Chapter 12, Review Exercises 8, 9, and 10.
3. [The following question is based mainly on Chapter13 of FPPA. Chapter 14 is needed only for the last part (but may help with some of the others).]

   A box contains six tickets, three marked with a star, and the other three marked with a diamond. Two draws will be made at random without replacement from this box.

   (a) Find the chance of getting a star on the first draw.

   (b) Find the chance of getting a star on the first draw and a star on the second draw.

   (c) Find the chance of getting a diamond on the first draw and a star on the second draw.

   (d) Find the chance of getting a star on the second draw.

   (e) Find the chance of getting a star at least once in the two draws.

   (f) True or false, and explain: the events "star on the first draw" and "star on the second draw" are independent.

   (g) True or false, and explain: the events "star on the first draw" and "star on the second draw" are mutually exclusive.

4. [The following question is based on Chapters 13 and 14 of FPPA. The problem description is lengthy, because it paints the big picture. The details you have fill in are fairly short.]

   The question is devoted to an analysis of a simplified version of a game that is played on the TV show "The Price is Right." In our game there are two players, you and me. The goal is to get the highest total number of spots for one or two roles of a fair die, without going over 6. (On TV, the game is played with 3 contestants and a glorified 20 sided die.)

   In more detail, our game is as follows. You start by rolling the die. Depending on the outcome of that roll, you can choose to roll the die again, or not. Your score is the total number of spots you roll. (For example, if your first roll is a 4 and you stop, your score is 4; but if your first roll is a 2 and you roll again and get a 5, your score is 7.) If your score is greater than 6, you lose (and I win). If your score is 6 or less, then I get to play, following the same rules. You win (and I lose) if my score is greater than 6, or less than or equal to your score. [The TV game allows ties, which are broken by a playoff; that complication is avoided here.]

   Some questions to be addressed are: (Q1) what should your strategy be --- when should you stop after the first roll, and when should you roll again; (Q2) what is the chance that you win the game? In connection with (Q1), note that if your first roll is "low", then you'd want to roll again to try to raise your score and make it harder for me to beat you. On the other hand, if your first roll is "high", then you'd want to stop, since a second role would likely take you over the limit of 6. But just what scores are "low", and which are "high"?

   Since we both want to win the game (and thus some neat prize), assume that we both play to our maximum advantage. For example, you shouldn't do something silly like roll a 6 and then roll again (in which case you'd turn a guaranteed win into a loss).

   (a) To begin the analysis, suppose that you've taken your turn and gotten a score of 3. The task at hand is to work out the chance that you win the game, conditional on your having this score. The only ways you can win are for me to:

   • roll a 1 the first time, and then roll a 1, 2, or 6; or
   • roll a ____ the first time, and then roll a ______ ; or
   • roll a ____ the first time, and then roll a ______ .

   Fill in the listing of the ways you can win. Are the ways mutually exclusive? Find the chance of your winning (show your work) and enter that number in the following table:

   Table I: Conditional chance for you to win, if your score is k.

   	k	Chance
   	1	0.0278
   	2	0.1111
   	3
   	4	0.4444
   	5	0.6944
   	6	1.0

   (b) Now let's back up a step. Suppose it is your turn and you have just rolled a 3 on your first roll. Whether you should stop or roll again depends on which option gives you the better chance of winning. If you stop, your score will be 3 and your chance to win is what you found in part (a). The task at hand is to work out your chance to win if you make the second roll. Assuming that you do make that roll, the only ways for you to win are for you to:

   • get a 1 on the second roll, and beat me with a score of 4; or
   • get a ____ on the second roll, and beat me with a score of ____ ; or
   • get a ____ on the second roll, and beat me with a score of ____ .

   Fill in the listing of the ways. Are the ways mutually exclusive? Find the chance of your winning (show your work) and enter that number in the following table:

   Table II: Conditional chance for you to win, if your first roll is k
   and you make another roll
   

   	k	Chance
   	1	0.4167
   	2	0.3982
   	3
   	4	0.2824
   	5	0.1667
   	6	0.0

   (c) Now it's time to write down your optimal strategy. Fill in the blank in the following table, and explain briefly.

   Table III: Whether you should roll again, if your first roll is k
   

   	k	Roll again?
   	1	Yes
   	2	Yes
   	3
   	4	No
   	5	No
   	6	No

   (d) Finally, it's time to work out the chance that you beat me. The ways you can do that are:

   • roll a 1 the first time, and beat me; or
   • roll a 2 the first time, and beat me; etc.

   Complete the listing of the ways. Are the ways mutually exclusive? Find the chance that you win the game (show your work).

   [Footnote: The game on TV can be simulated with a 20-sided die, with faces numbered from 1 to 20. There are three contestants, A, B, and C. A goes first, then B, then C. The one with the highest total not exceeding 20 for one or two spins wins. A tie for the highest total is broken by a playoff that gives each participant an equal chance to win.

   The optimal strategies are as follows:

   • A should spin again if her/his first spin is <= 13.

   • If A's total is j (= 0 if s/he's already out of the game), then B should spin again if her/his total is <=
     10, if 0 <= j <= 10,
     j, if 11 <= j <= 13,
     j-1, if 14 <= j <= 20.
     

   • C should spin again if her/his first spin is lower than the current high score. If her/his first score k ties the current high score, s/he should spin again if: k <= 10 and there's a two way tie, or k <= 13 and there's a three way tie.

   If the players all use their optimal strategies, their chances of winning are: A, 30.8%, B, 33.0%; C, 36.2%. The game is nearly fair, although C has a slight edge over B, and B a slight edge over A.]

Homework 3: due Wednesday 4/23

1. Ten students from this course were selected at random and asked the heights of their fathers and mothers. The results (in inches) were:

   		Father's Height	Mother's Height
   		67	62
   		72	64
   		67	65
   		71	68
   		70	63
   		72	65
   		67	60
   		64	66
   		74	61
   		72	71
   	Average	69.6	64.5
   	SD	3.01	3.14

   (a) What height would you predict for the mother of a student in the class, if you didn't know the father's height? Explain briefly.

   (b) Draw the scatter diagram of Mother's Height (vertical axis) on Father's Height (horizontal axis). Use a sheet of graph paper. How would you characterize the relationship between these two variables?

   (c) Suppose the father of a student in the class is 73 inches tall. How tall would the student's mother have be to lie on the SD line?

   (d) On your scatter diagram, mark the point of averages and draw (use a straight edge) the SD line. Clearly label the point and the line.

   (e) Calculate the correlation between Father's Height and Mother's Height.

   (f) For the student in part (b), calculate the regression estimate of the mother's height.

   (g) Draw the regression line for predicting Mother's Height from Father's Height on your scatter diagram. Clearly label the line.

   (h) Which line, the SD line or the regression line, appears to do a better job at predicting Mother's Height from Father's Height, for this data set. Explain briefly.

   (i) Roughly speaking, how useful is Father's Height for predicting Mother's Height?

2. A study was made of the relationship between miles per gallon (Mpg) and horsepower (Hpw) for some 400 different kinds of cars. Mpg is plotted against Hpw in the scatter plot on the left below. On the right, log10(Mpg) is plotted against log10(Hpw). Here log10(x) stands for the common (base 10) logarithm of the number x; for example, log10(10) = 1.00, log10(20) = 1.30, log10(30)= 1.48 , log10(50) = 1.70, log10(100) = 2.00, log10 (150) = 2.18, and log10(200) = 2.30.
   

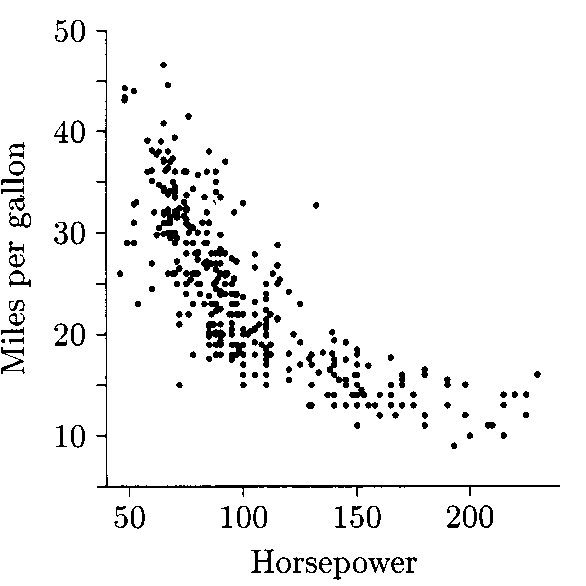
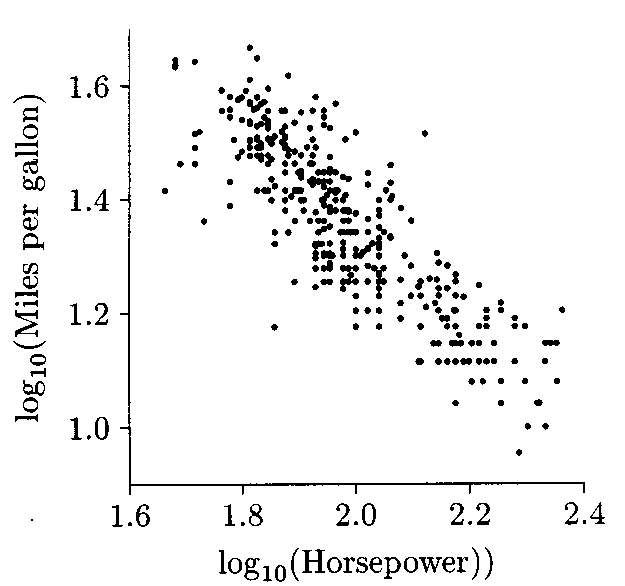
   (a) Would it be appropriate to use the regression method to predict Mpg from Hpw? Explain briefly. (b) Would it be appropriate to use the regression method to predict log10(Mpg) from log10(Hpw)? If so, how could you then predict Mpg from Hpw? Explain briefly.

3. FPPA, Chapter 8, Review Exercises 1 and 5.
4. FPPA, Chapter 9, Review Exercises 4 and 13.
5. FPPA, Chapter 10, Review Exercises 3, 4, and 5.
6. FFPA, Chapter 10, Review Exercise 6, but change part (c) to 25%, and part (d) to 90%.

Homework 2: due Weds 4/16